本文重点参考了文章Mamba: The Hard Way和开源项目flash-linear-attention。
Prefill与Decoding
我们都知道,在Attention的计算中,Prefill和Decoding是两个不同的场景,具体特性如下:
| 特性 | Prefill | Decoding |
|---|---|---|
| 输入 | 长序列(长度 $L$) | 1 个新 token + 历史状态 |
| 常见瓶颈 | Compute bound(Tensor Core 利用) | Memory/Latency bound(状态读写 + 小矩阵计算) |
在回忆一下理论篇的介绍,特别是关于Mamba章节中的推导,常见的Linear Attention有两种表示格式:
矩阵格式(Attention视角):
$$ y_i = \sum_{j=0}^i (CausalMask(Q_i K_j^T)) V_j $$
递推格式(SSM视角):
$$ h_t = A_t h_{t-1} + B_t x_t $$ $$ y_t = C h_t $$
其中Decoding的算子可以比较直接的使用递归格式进行计算,因此我们本文重点还是看Prefill的实现。
Linear Attention常见算法
在Linear Attention的计算中,有一些常见的思路,本章结合flash-linear-attention的实现,对这些思路进行讲解。
Prefix Scan / Cumsum 前缀和
算法简介
先讲一下什么是Prefix Scan算法,简单来说Prefix是针对有结合性的算子提出的一种优化方式
假设有 $y_t = x_1 ⊗ x_2 ⊗ x_3 … ⊗ x_t$, 如果⊗支持结合律,那么y_t就可以用一个简单的Reduce进行求解
=== Parallel Prefix Scan (Up Sweep) ===
序列: [x1][x2][x3][x4][x5][x6][x7][x8]
Step 1: 相邻元素两两合并 (4 次并行操作)
[x_1] [x1 ⊗ x2] [x_3] [x3 ⊗ x4] [x_5] [x5 ⊗ x6] [x_7] [x7 ⊗ x8]
Step 2: 继续合并 (2 次并行操作)
[x_1] [x_1 ⊗ x_2] [x_3] [x1 ⊗ x2 ⊗ x3 ⊗ x4] [x_5] [x5 ⊗ x6] [x_7] [x5 ⊗ x6 ⊗ x7 ⊗ x8]
Step 3: 最终合并 + Down-sweep (恢复所有前缀和)
[完整的前缀和序列(y_t)]
总计: O(log L) 轮,每轮 O(L) 次操作
我们把这个步骤称为Up Sweep,这个过程中我们不仅计算了最终的$y_t$,也产生了很多中间结果,我们可以把这个数组看成一个二叉树。 回忆一下,我们要算的可能不只有最终的 $y_L$,我们想计算所有的 $y_1$ 到 $y_L$。如果只用 Up Sweep,我们只能得到最后一个位置的完整前缀和。为了高效地得到所有位置的前缀和,我们需要引入 Down Sweep 阶段。
Down Sweep 的核心思想是:利用 Up Sweep 阶段在树节点中留下的中间结果,从根节点开始向下分发“左侧累加值”信息。
=== Parallel Prefix Scan (Down Sweep) ===
Up Sweep 后的状态: [x1] [x1⊗x2] [x3] [x1⊗x2⊗x3⊗x4] [x5] [x5⊗x6] [x7] [x1⊗...⊗x8]
Step 1: 置零 (Set to Identity)
将最后一个元素(根节点)设为单位元(如 0)。
这是因为第一个元素的前缀和应该是 0。
[x1] [x1⊗x2] [x3] [x1⊗x2⊗x3⊗x4] [x5] [x5⊗x6] [x7] [0]
Step 2: 交换与分发 (Swap and Sum)
从上往下,每一层进行如下操作:
1. 暂存当前节点的左孩子值。
2. 将当前节点的值赋给左孩子。
3. 将“暂存的左孩子值 ⊗ 当前节点值”赋给右孩子。
(第一轮分发:将根节点的 0 传给左半区,将左半区的总和传给右半区)
[x1] [x1⊗x2] [x3] [0] [x5] [x5⊗x6] [x7] [x1⊗x2⊗x3⊗x4]
Step 3: 递归向下 (Recursive Down)
继续向下重复此过程,直到叶子节点。
最终数组会变成 Exclusive Scan 序列(即每个位置存储它之前所有元素的和)。
Step 4: 恢复 Inclusive Scan
将 Exclusive Scan 的结果与原始序列对应位置进行 ⊗ 操作,即可得到 y_1 到 y_L。
总计: O(log L) 轮,每轮 O(L) 次操作,总复杂度依然是 O(L)。
这两个过程可以从两个个树型的计算来表示:
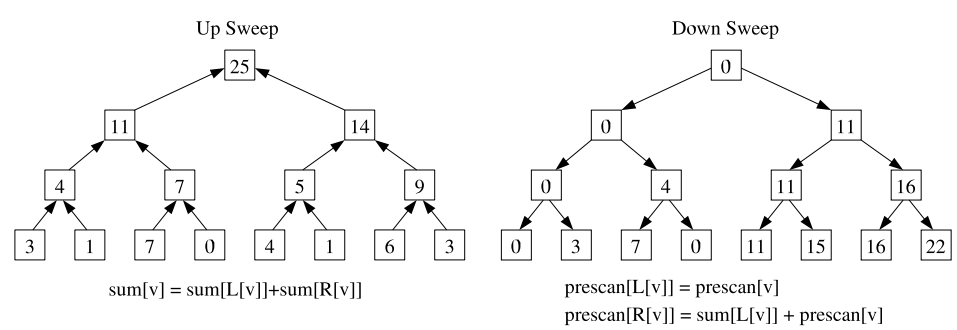
顺带的,给出一个例子:
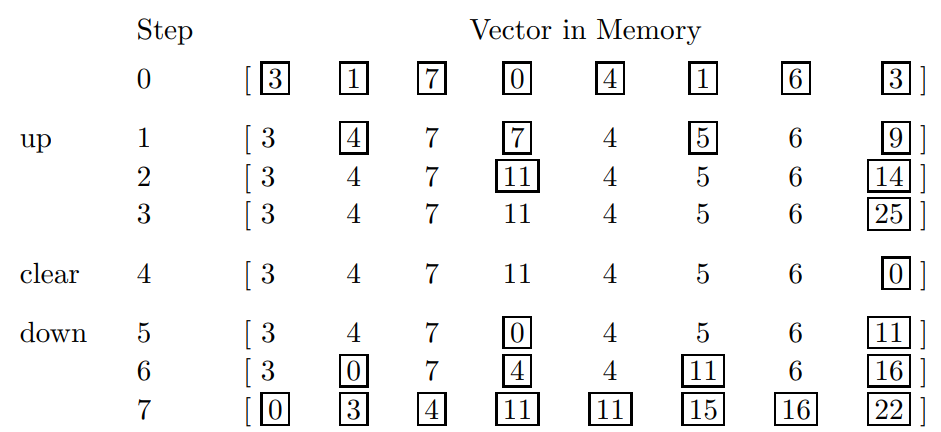
Linear Attention的Prefix Scan
了解了 Prefix Scan 算法,我们来看一下 Linear Attention 的递推公式:
$$ h_t = A_t h_{t-1} + B_t x_t $$ $$ y_t = C h_t $$
这个公式描述了一个一阶线性递推过程。在传统的 RNN 中,我们需要串行地计算 $h_1, h_2, \dots, h_L$,这在训练长序列时会成为严重的瓶颈。为了将其转化为 Prefix Scan,我们需要找到一个结合律算子 $\otimes$。
数学推导:线性递推的结合律
为什么线性递推可以转化为 Prefix Scan?关键在于将状态转移看作是线性函数的复合。
对于任意时刻 $t$,状态更新公式为: $$ h_t = A_t h_{t-1} + b_t \quad (\text{其中 } b_t = B_t x_t) $$
我们可以将这个过程看作是一个线性变换 $f_t(h) = A_t h + b_t$。那么 $h_t$ 实际上是这些变换的连续嵌套: $$ h_t = f_t(f_{t-1}(\dots f_1(h_0) \dots)) $$
如果我们定义一个算子 $\otimes$ 来表示两个线性变换的复合 $f_j \circ f_i$(假设 $j > i$,即 $j$ 是较晚的时刻): $$ (f_j \circ f_i)(h) = A_j (A_i h + b_i) + b_j = (A_j A_i) h + (A_j b_i + b_j) $$
因此,我们可以定义元组 $(A, b)$ 上的算子 $\otimes$: $$ (A_j, b_j) \otimes (A_i, b_i) = (A_j A_i, A_j b_i + b_j) $$
这个算子的物理意义是:它计算了从状态 $h_{i-1}$ 到 $h_j$ 的“总转移矩阵”和“总偏置项”。 当我们对序列 $[(A_1, b_1), (A_2, b_2), \dots, (A_L, b_L)]$ 执行 Prefix Scan 时,第 $t$ 个位置的结果 $(A_{1:t}, b_{1:t})$ 就代表了从初始状态 $h_0$ 到 $h_t$ 的完整变换参数: $$ h_t = A_{1:t} h_0 + b_{1:t} $$
证明结合律: 假设有三个连续的状态转移 $(A_3, b_3), (A_2, b_2), (A_1, b_1)$:
- 左结合:$((A_3, b_3) \otimes (A_2, b_2)) \otimes (A_1, b_1) = (A_3 A_2, A_3 b_2 + b_3) \otimes (A_1, b_1) = (A_3 A_2 A_1, (A_3 A_2) b_1 + (A_3 b_2 + b_3))$
- 右结合:$(A_3, b_3) \otimes ((A_2, b_2) \otimes (A_1, b_1)) = (A_3, b_3) \otimes (A_2 A_1, A_2 b_1 + b_2) = (A_3 A_2 A_1, A_3 (A_2 b_1 + b_2) + b_3)$
展开后可以发现两者完全一致。这意味着我们可以使用 Parallel Prefix Scan 在 $O(\log L)$ 的时间内并行计算出所有的 $h_t$。
代码实现参考
在 flash-linear-attention 或 Mamba 的实现中,通常会利用 jax.lax.associative_scan 或在 Triton 中手动实现类似的逻辑。以下是一个简化的逻辑示例:
def associative_scan_op(q_earlier, q_later):
"""
q = (A, b)
计算两个线性变换的复合: f_later(f_earlier(h))
"""
a_i, b_i = q_earlier
a_j, b_j = q_later
# 新的 A 是两个矩阵的乘积 (注意顺序: 晚的在左)
# 新的 b 是 晚的A * 早的b + 晚的b
return a_j * a_i, a_j * b_i + b_j
# 1. 准备输入元组序列
# A_bars: [L, d_state]
# b_bars: [L, d_state], 即 B_t * x_t
inputs = (A_bars, b_bars)
# 2. 执行并行前缀扫描
# 返回每个位置 t 从 h_0 到 h_t 的总变换参数 (A_1:t, b_1:t)
combined_params = associative_scan(associative_scan_op, inputs)
# 3. 计算隐藏状态 h_t (假设 h_0 = 0)
# h_t = A_1:t * h_0 + b_1:t = b_1:t
h_states = combined_params[1]
# 4. 计算输出 y = C * h
outputs = C * h_states
这种表示法的精妙之处在于,它将原本必须串行执行的 for 循环($h_t$ 依赖 $h_{t-1}$)转化为了树状的并行规约过程。在 GPU 上,这意味着我们可以利用数千个核心同时处理序列的不同部分,极大地提升了 Prefill 阶段的吞吐量。
Chunk-wise Parallel:分块并行
Chunk wise Parallel 是 flash-linear-attention 中最核心的 Prefill实现方式包括Mamba the hard way也是在讲解这一思想,虽然这一思想在具体实现时根据Kernel的划分可以有多种不同的实现方式,但是其核心思想始终都是 Two-pass:
具体来说,我们把整个要计算的序列(长度L)拆分成多个不同的Chunk(长度C),然后按照进行计算:
- Pass 1:计算每个 Chunk 的最后一个token的隐藏状态(顺序计算,一共$L/C$ 步,产生 $L/C$ 个状态)
- Pass 2:在Chunk 内做局部计算 + 叠加来自前序 Chunk 的状态贡献(并行计算、MatMul 密集)
该计算过程可以用下图表示:
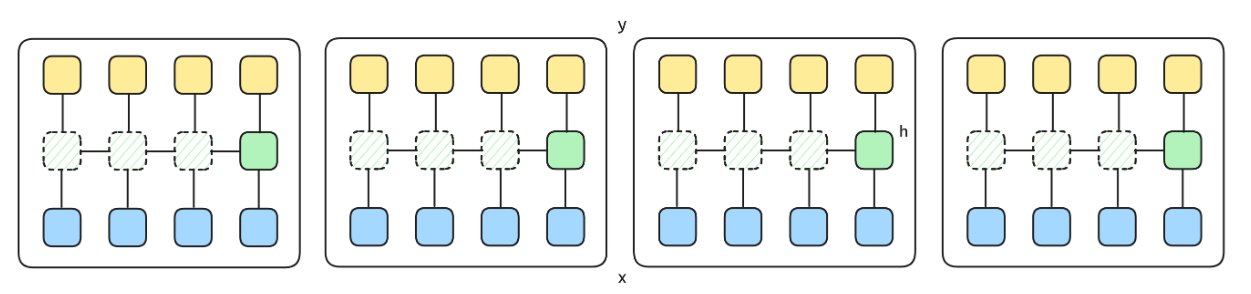
- 第一遍Pass顺序对每个Chunk进行计算,得到所有深绿色方块。
- 第二遍Pass同时在Chunk内先基于深绿色方块来计算所有浅绿色方块,然后计算最终要输出的蓝色方块。
Triton 伪代码
# 1. Inter-chunk: 状态传递 (Pass 1)
# 类似于 RNN,但只在 Chunk 边界进行
for i in range(num_chunks):
# 加载上一个 Chunk 的状态 (i=0 时为初始状态 S_0)
b_s = tl.load(s_ptr + (i - 1) * stride) if i > 0 else tl.zeros(...)
# 更新状态:S = S * Decay + K^T * V (当前 Chunk 的贡献)
b_s = b_s * chunk_decay + tl.dot(tl.trans(b_k_block), b_v_block)
# 保存状态供下一个 Chunk 使用
tl.store(s_ptr + i * stride, b_s)
# 2. Intra-chunk: 块内并行计算 (Pass 2)
# 类似于标准 Attention,但只看 Chunk 内部
# 加载当前 Chunk 的 Q, K, V
b_q = tl.load(q_ptr) # [BLOCK_SIZE, D_K]
b_k = tl.load(k_ptr) # [BLOCK_SIZE, D_K]
b_v = tl.load(v_ptr) # [BLOCK_SIZE, D_V]
# 计算局部 Attention Score: Q @ K^T
b_s = tl.dot(b_q, tl.trans(b_k)) * decay_mask # [BLOCK_SIZE, BLOCK_SIZE]
# 计算输出
b_o = tl.dot(b_s, b_v) # [BLOCK_SIZE, D_V]
# 加上来自前一个 Chunk 状态的贡献
b_o += tl.dot(b_q, prev_s) * decay
FFT和卷积型线性注意力
核心思想:卷积加速
对于某些Linear Attention变体(如Hyena),其特殊之处在于:衰减权重只依赖于相对位置,而不是绝对位置。这意味着我们可以把计算转化为卷积操作,从而利用FFT加速。
从递推到卷积
考虑一个简化的输出公式: $$o_t = \sum_{j=1}^t u_j \cdot \alpha_{t-j}$$
其中:
- $u_j$ 是时刻 $j$ 的输入表示
- $\alpha_{t-j}$ 是只依赖于距离 $(t-j)$ 的衰减系数
可以看到这里$\alpha$ 的下标是 $t-j$(相对距离),和卷积的定义是可以对上的。
直接计算卷积的复杂度是 $O(L^2)$(对每个位置 $t$,都要累加前面所有的 $j$)。但根据卷积定理:
$$\text{时域卷积} = \text{频域点乘}$$ $$f * g = \mathcal{F}^{-1}(\mathcal{F}(f) \cdot \mathcal{F}(g))$$
FFT的复杂度是 $O(L \log L)$,频域点乘是 $O(L)$,总复杂度 $O(L \log L)$ 远小于 $O(L^2)$。
举一个具体的例子:
假设序列长度 $L=4$,输入 $u = [1, 2, 3, 4]$,衰减核 $\alpha = [1.0, 0.5, 0.25, 0.125]$(距离越远衰减越强)。
直接计算($O(L^2)$):
o_1 = u_1 * α_0 = 1 * 1.0 = 1.0
o_2 = u_2 * α_0 + u_1 * α_1 = 2*1.0 + 1*0.5 = 2.5
o_3 = u_3 * α_0 + u_2 * α_1 + u_1 * α_2 = 3*1.0 + 2*0.5 + 1*0.25 = 4.25
o_4 = u_4 * α_0 + u_3 * α_1 + u_2 * α_2 + u_1 * α_3 = 4*1.0 + 3*0.5 + 2*0.25 + 1*0.125 = 6.125
FFT加速($O(L \log L)$):
1. FFT(u) 和 FFT(α) → 转到频域(O(L*logL))
2. 频域点乘 → 逐元素相乘(O(L))
3. IFFT → 转回时域(O(L*logL))
代码实现
def fft_conv(u, k, seqlen):
"""
使用 FFT 加速因果卷积计算
参数:
u: 输入序列 [batch, seqlen, dim]
k: 衰减核 [seqlen] (只依赖相对位置)
seqlen: 序列长度
返回:
输出序列 [batch, seqlen, dim]
"""
# 1. 补零到 2*L (避免循环卷积的边界问题)
fft_size = 2 * seqlen
# 2. FFT 变换到频域 (O(L log L))
k_f = torch.fft.rfft(k, n=fft_size) # 衰减核
u_f = torch.fft.rfft(u, n=fft_size) # 输入信号
# 3. 频域点乘 (O(L)) -> 这一步替代了原本 O(L^2) 的时域卷积。
y_f = u_f * k_f
# 4. IFFT 逆变换回时域 (O(L log L))
y = torch.fft.irfft(y_f, n=fft_size)
# 5. 截取有效部分(去掉补零部分)
return y[..., :seqlen]
虽然看上去FFT是一个很好的算法,但是因为大部分的Linear Attention变体的衰减核不只和位置有关(会受到输入x影响),因此,FFT加速现在并不常见,只在特定架构中有效。
进一步的计算效率与性能优化
Delta Net:WY表示与UT变换
我们在前文中讲解了基础的Chunk Wise算法框架,但是在实践中这个框架并不能直接out-of-box的拿出来使用,这里以Delta Net为例讲解一下WY表示和UT变换(KDA中也使用了类似的方法)
先回顾一下 Chunk-wise 算法的核心思想(Two-pass):
Pass 1 (Inter-chunk):顺序计算每个 Chunk 的边界状态
- 对于传统 Linear Attention:$S[i+1] = S[i] + V[i]^T K[i]$(矩阵乘法,高效)
Pass 2 (Intra-chunk):并行计算 Chunk 内部的输出
- 需要把 Chunk 内的局部累积效果表示成矩阵乘法形式
- 例如:$O[i] = Q[i] S[i]^T + (\text{Chunk内部的局部贡献})$
为了提高计算效率,这两个 Pass 都会希望计算必须能表示成高效的矩阵乘法(可以利用 GPU Tensor Core),而不是串行循环或者稠密的 $d \times d$ 矩阵加减法操作。
DeltaNet 原始形式的问题
在传统的 Linear Attention 中,状态更新是简单的加法:$S_t = S_{t-1} + v_t k_t^T$。
- Chunk 内累积:$S[i+1] = S[i] + \sum_{t=1}^{C} v_t k_t^T = S[i] + V^T K$
但是回忆一下理论篇的推导,在 DeltaNet 中, Delta Rule的更新规则会更加复杂: $$ S_t = S_{t-1}(I - \beta_t k_t k_t^{\top}) + \beta_t v_t k_t^{\top} $$
现在让我们尝试在 Chunk 内做累积,就会发现很多计算效率上的问题:
经过论文Parallelizing Linear Transformers with the Delta Rule over Sequence Length中Section 2的公式推导,可以发现在一个 Chunk 内,从 $S[i]$ 到 $S[i+1]$ 的更新公式为:
$$ S[i+1] = S[i] \prod_{t=1}^C \bigl(I - \beta_t k_t k_t^{\top}\bigr) + \sum_{t=1}^C \left( \beta_t v_t k_t^{\top} \prod_{j=t+1}^C \bigl(I - \beta_j k_j k_j^{\top}\bigr) \right). $$
其中符号含义:
- $C$:Chunk size(每个 Chunk 的长度)
- $S[i]$:第 $i$ 个 Chunk 的输入状态
- $S[i+1]$:第 $i$ 个 Chunk 的输出状态(传递给下一个 Chunk)
- $t$:当前 Chunk 内的位置索引($t = 1, 2, \dots, C$)
- $k_t, v_t$:第 $i$ 个 Chunk 内第 $t$ 个位置的 key 和 value
- $\beta_t$:第 $i$ 个 Chunk 内第 $t$ 个位置的学习率/遗忘门
还有公式种两个项的含义:
- 第一项:前一个 Chunk 的状态 $S[i]$ 经过当前 Chunk 内所有 Delta 更新的累积衰减
- 第二项:当前 Chunk 内每个位置 $t$ 的贡献 $\beta_t v_t k_t^T$,并经过后续位置 $j > t$ 的衰减
基于这个公式,如果我们直接计算 $P[i] = \prod_{t=1}^C (I - \beta_t k_t k_t^T)$:
- 展开两个矩阵的乘积:$(I - \beta_2 k_2 k_2^T)(I - \beta_1 k_1 k_1^T) = I - \beta_2 k_2 k_2^T - \beta_1 k_1 k_1^T + \beta_1\beta_2 k_2 k_2^T k_1 k_1^T$
- 继续乘下去,交叉项会越来越多,经过 $C$ 步,结果变成一个秩为 $O(C)$ 的稠密矩阵
对于这种方式计算 $P[i]$ 是非常低效的–>因为我们无法高效计算和存储这个计算过程:需要 $O(d^2)$ 的空间,计算复杂度是 $O(Cd^3)$
解决方案:WY 表示 + UT 变换
WY 表示:让 Chunk 累积可以用矩阵乘法表示
可以看到,高秩矩阵值的状态对于chunk-wise的计算和存储都是一个很大的挑战,因此我们需要引入一些变换来解决这个问题。
针对DeltaNet,一个关键的发现是:虽然直接计算 $\prod (I - \beta_t k_t k_t^T)$ 会秩爆炸,但利用 Householder 变换的数学性质,这个连乘依然可以紧凑地表示为: $$ \prod_{i=1}^C \bigl(I - \beta_i k_i k_i^{\top}\bigr) = I - W_C K_C^{\top}, $$ 其中 $W_C \in \mathbb{R}^{C \times d}$,$K_C \in \mathbb{R}^{C \times d}$。
这样,Inter-chunk 更新就变成了: $$ S[i+1] = S[i] \bigl(I - W[i] K[i]^{\top}\bigr) + U[i]^{\top} K[i] = S[i] - (S[i]W[i])K[i]^{\top} + U[i]^{\top} K[i] $$
这是一个标准的矩阵乘法,我们可以更好地利用Tensor Core, 计算复杂度 $O(Cd^3)$ 降到了 $O(Cd^2)$,同时状态空间也从 $O(d^2)$ 变成了 $O(dC)$。大大降低了计算和存储IO的负担。
UT 变换:让 W 的计算也能并行化
但是,$W$ 矩阵中的每一行 $w_t$ 的计算仍然还是递归的: $$ w_t = \beta_t \Bigl(k_t - \sum_{i=1}^{t-1} w_i (k_i^{\top} k_t)\Bigr) $$
这又是串行计算,无法利用 Tensor Core。
UT 变换通过定义下三角矩阵 $A$(包含 $k_i^T k_j$ 的信息),将递归转化为: $$ W = T \mathrm{diag}(\beta) K, \qquad \text{其中 } T = (I - A)^{-1} $$
由于 $A$ 是严格下三角,$T$ 可以通过前向替换高效求解,或者在 Chunk 较小时直接用矩阵乘法,于是:
- 计算变成了矩阵运算,可以调用GPU Tensor Core加速计算
- 在 Chunk 内并行处理,不在需要一步步串行计算
WY 表示 + UT 变换将 DeltaNet 的 Chunk 内计算转化为了 GPU 友好的矩阵乘法,这让DeltaNet的 Chunk-wise 并行算法真正可行。
性能测试与分析
最后,我在半张H200(H200 MIG3-70G)的GPU上对上面的算法做了一些性能测试:
SIMPLE GLA性能测试
算法特性
Simple GLA 相比完整的 GLA,采用了 head-wise gating 而非 elementwise gating。这一简化减少了参数量,也降低了数值不稳定的概率。
其状态更新公式为: $$S_{t+1} = g_{t+1} \odot S_{t} + K_{t+1} V_{t+1}^{\top}$$ 其中 $g$ 是一个标量,这使得衰减操作可以高效地融合到矩阵计算中。
性能测试对比
测试配置:Batch=4, Heads=8, d_head=128, 对不同的序列长度L进行测试:
测试一共使用了3种算法:
- Chunk-wise算法: 使用2个Kernel的Chunk-wise算法
- Fused Chunk-wise算法: 使用1个Kernel的Chunk-wise算法
- Parallel Scan:基于Sweep Up/Down的算法
| L | Chunk-wise | Fused Chunk-wise | Parallel Scan |
|---|---|---|---|
| 32 | 0.099184 | 0.045680 | 0.013440 |
| 64 | 0.093040 | 0.044832 | 0.018016 |
| 128 | 0.113344 | 0.070464 | 0.020704 |
| 256 | 0.111024 | 0.112288 | 0.034528 |
| 512 | 0.172096 | 0.281088 | 0.064032 |
| 1024 | 0.498624 | 0.546480 | 0.150272 |
| 2048 | 0.985968 | 1.078208 | 0.422528 |
| 4096 | 1.955248 | 2.132128 | 1.350048 |
| 8192 | 3.882000 | 4.229376 | 4.766928 |
| 16384 | 7.750400 | 8.427360 | 17.839392 |
可以看到,在序列较短时(例如 $L\le 4096$),Parallel Scan 的优势更明显;这主要来自两点:
- 并行 scan 的关键路径是 $O(\log L)$ 轮的 up-sweep/down-sweep,短序列时轮数少;
- 这类实现往往可以把“状态合并”写成很轻量的向量/小矩阵算子,kernel 本身更偏 latency-bound,短 $L$ 时更容易占优。
但是随着序列变长(从表中可见在 $L\approx 8192$ 附近出现拐点,$L=16384$ 时差距被明显拉开),Parallel Scan 会逐渐变慢,原因通常是:
- 需要的 sweep 轮数随 $\log L$ 增长,并且每一轮都伴随全局同步/跨 block 的数据交换,整体更偏 memory-bound;
- scan 的算术强度相对较低,序列越长越容易被 HBM 带宽与同步开销限制。
相比之下,Chunk-wise 的 Two-pass 结构在长序列时更“吃得满” Tensor Core:Pass 1 只在 chunk 边界更新状态、Pass 2 在 chunk 内做更大粒度的矩阵运算(更高的 arithmetic intensity),因此随 $L$ 增长时吞吐更稳定。
另外,Fused Chunk-wise 虽然只需要启动一次 Kernel,但它往往需要在一个 kernel 内同时承担 Pass 1 + Pass 2 的职责:为了避免中间状态落到显存,必须把更多的中间量/状态(例如每个 head 的累计状态 $S$ 或 chunk 边界状态)尽可能保存在寄存器中。 这会带来寄存器压力上升与 occupancy 下降,极端情况下还会触发 register spill(溢出到 local memory),从而在长序列时反而不如两 Kernel 的 Chunk-wise 实现。
Delta Net性能测试
这节我们以 Delta Net 为例,先给出核心的性能对比结果,然后解释为什么某些并行化策略(特别是基于Parallel scan 的方法)在实践中会失败。
对于不同的序列长度L,运行的结果表现如下:
| L | Chunk-wise Parallel | Parallel Scan |
|---|---|---|
| 128 | 0.178384 | 0.159504 |
| 256 | 0.172256 | 0.159840 |
| 512 | 0.185056 | 0.210512 |
| 1024 | 0.198560 | 0.478272 |
| 2048 | 0.350336 | 1.239392 |
| 4096 | 0.674592 | 3.765408 |
| 8192 | 1.318208 | 12.916416 |
| 16384 | 2.600304 | 47.368912 |
性能测试对比分析
可以看到在Delta Net种,Parallel Scan算法的优势明显变小,在L=512时候就被Chunk-wise的算法反超了。
为了看清 Parallel Scan 需要合并的是什么,我们把 DeltaNet 的单步更新再写一遍:
$$ S_t = S_{t-1}(I - \beta_t k_t k_t^{\top}) + \beta_t v_t k_t^{\top}. $$
然后,记
$$M_t = I - \beta_t k_t k_t^{\top} \in\mathbb{R}^{d\times d}$$
$$B_t = \beta_t v_t k_t^{\top} \in\mathbb{R}^{d\times d}$$
于是每一步都是对矩阵S的仿射变换:
$$S_t = S_{t-1} M_t + B_t$$
要把这个过程用Parallel Scan加速,我们可以继续使用前文种定义的算子 $\otimes$ :
$$(A_j,b_j)\otimes (A_i,b_i) = (A_j A_i,; A_j b_i + b_j),$$
它表示先做时刻 $i$ 的变换再做时刻 $j$ 的变换。将该算子应用到序列 $(M_t,B_t)$ 后:
$$S_1 = S_0 M_1 + B_1$$ $$S_2 = S_1 M_2 + B_2 = S_0 (M_1 M_2) + (B_1 M_2 + B_2)$$
可以看到,在合并一段区间时需要把对应的 $M$ 矩阵相乘(产生 $M_1M_2$),同时把先前的 $B$ 按新的 $M$ 变换后累加(产生 $B_1M_2+B_2$),这是两个比较重的矩阵操作,也是Delta Net的Parallel Scan算法效率不高的根本原因:
-
合并里必须显式算/存 $M$: 对普通线性注意力(加法累积)而言,scan 合并的是固定形状的小矩阵/向量,算子很轻。 但 DeltaNet 合并的是矩阵 $M_t$ 是 $d\times d$,而且要在合并时做 $M_1M_2$等运算,复杂度要高得多。
-
难以通过低秩假设优化计算: 单步 $M_t = I - \beta_t k_t k_t^T$ 是 rank-1 更新(把一个已有矩阵加上或减去一个rank为1的矩阵);但两步相乘: $$ (I - \beta_2 k_2 k_2^T)(I - \beta_1 k_1 k_1^T) = I - \beta_1 k_1 k_1^T - \beta_2 k_2 k_2^T + \beta_1\beta_2 k_2 (k_2^T k_1) k_1^T $$ 最后的交叉项会不断出现。把一段长度为 $m$ 的连乘写成“单位阵减低秩”的形式时,其有效秩一般会随 $m$ 增长(直观上接近 $O(m)$)。 这意味着:如果 scan 想只携带低秩因子(比如 $I - W K^T$),那么在 up-sweep 的更高层节点里,$W,K$ 的行数会越来越大——中间态不再是常数大小,从而无法像普通 scan 那样用固定 shape 的张量高效实现。
Parallel Scan 虽然只有 $O(\log L)$ 轮,但每一轮都要对整段序列做一次“合并 + 全局读写/同步”,当合并算子本身已经是大矩阵操作时,就会表现出你表里那种随长度急剧变慢的趋势。
总结
可以看到,在Linear Attention中,虽然有着多重不同的工程实现方式,但是具体到特定的算子,还是需要根据算子的特性和计算的参数(如序列长度)来选择最合适的算法。
Last modified on 2026-01-01