**         **一元线形回归模型：有变量x,y。假设有关系y=c+bx+e,其中c+bx 是y随x变化的部分，e是随机误差。

可以很容易的用函数lm()求出回归参数b,c并作相应的假设检验，如：

x<-c(0.10, 0.11, 0.12, 0.13, 0.14, 0.15,0.16, 0.17, 0.18, 0.20, 0.21, 0.23)
y<-c(42.0, 43.5, 45.0, 45.5, 45.0, 47.5,49.0, 53.0, 50.0, 55.0, 55.0, 60.0)
lm.sol<-lm(y ~ 1+x)
summary(lm.sol)

仅列出部分返回结果：

Residuals:

  Min       1Q   Median    3Q     Max

-2.0431  -0.7056  0.1694  0.6633  2.2653

Coefficients:

            Estimate Std. Error      t value   Pr(>|t|)

(Intercept)   28.493      1.580   18.04    5.88e-09 ***

x            130.835      9.683   13.51 9.50e-08 ***

在我们的输入中，关键是lm.sol<-lm(y ~ 1+x)的调用，这里可以看到，lm使用了参数y~1+x,即表示我们使用的是模型y=c+bx+e (1表示常数项)

然后我们使用summary查看了lm返回的结果。在Residuals:中，我们可以看到的是一些关于残差的信息：最小最大值，4分位数等。Coefficients:中则是最为关键的对c和b的相关估计。其中Estimate是与b,c值的估计，Std. Error 则是回归参数b和c的标准差：sd(b), sd(c)。剩下的两个参数则是对回归参数的假设检验： t value是对b,c进行假设检验的t值，以及P-值(用来与显著性水平比较决定是否接受该阿假设检验)Pr(>|t|)。最后我们还可以看到3个* 号，这表明x和y有非常显著的线性关系(*可以有0—3个，越多则线性关系越显著)。

做毕设的时候写的东西，贴上来吧…………

由于在OPENGL只能通过程序语言绘制模型，远不能达到可见既可得的目的。因此，比起3DMAX、MAYA等可视化3D建模工具，OPENGL模型的建立就相当的困难，为了简化这一问题的处理，可以使用简单小巧的MS3D来完成可见即可得的绘制过程。

MS3D的文件有着非常简单良好的文件结构，可从该文件中完美读取在可视工具中绘制的3D图形模型包含的点、线、面等各项基本结构的参数与位置，并在OPENGL根据读取结果即可进行绘制重现该模型。

MS3D全名为MilkShape3D，是一款简单小巧的3D可视化图形建模工具，可以简单的使用各种点、线面等基本图形元素组合建立模型，并进行贴图，分组。进一步的，该工具还支持简单的骨骼动画制作，是一款非常好用的3D图形构建工具。

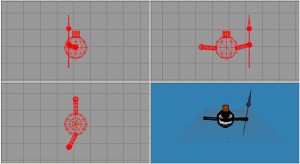[][1]

在建立了MS3D中完成模型建立后可保存为.ms3d的文件格式，通过对该文件格式进行分析，就可以了解文件结构，以在程序中通过读取该文件重现所见模型。

该文件依次包括6段信息，除第一段文件头外，其它每段的开始位置都记录了该段中元素的数目，可用于计算该段的具体大小。

• 文件头:大小固定为14字节。前10个字节为固定的标志 MS3D000000<-其中后6个字节就是字符0（即值为48）后4个字节为该模型格式的版本号，这4个字节为一个有符号整数，目前该版本号的值为3或4，两种版本的格式细节不同。

• 点数据：紧接着文件头的就是模型的顶点数据部分，顶点部分的头两个字节为一个无符号整数，表示有多少个顶点。之后便是一个接一个的顶点的具体数据，包括可见性，x,y,z的坐标和绑定骨骼的ID编号(未绑定骨骼则为-1)。

• 多边形数据: 紧接着顶点数据的是多边形数据（三角形），多边形部分头两个字节是一个无符号整数，表示有多少个三角形。之后便是一个接一个的三角形数据。主要记录了每个三角形结构，包括顶点索引，顶点法线（用于光照计算），纹理坐标和组信息。

• 组信息：即网格信息，出于灵活性的考虑，模型的一个个三角形被按照网格或是组来划分。网格部分头两个字节是一个无符号整数，表示有得多少个网格。之后便是一个接一个的网格数据，每个网格结构的大小可能不同（因为他们拥有的三角形数不同）。主要包括网格的名字（字符串），三角形数量、三角形索引和材质索引（无材质则为-1）。

• 材质信息：贴图、颜色等材质部分。头两个字节是一个无符号整数，表示有多少个材质。之后便是一个接一个的材质信息。包括材质名、环境光、漫射光、高光、自发光、发光值、透明度、贴图文件名、透明贴图文件名。

• 骨骼信息： 动画、动作等。该结构是MS3D中的动态结构，仅当建立动态动画时存在，包括一种名为关键帧的结构，记录时间与对应的坐标系变换。骨骼信息，一开始是两个字节的无符号整数，表示一共有多少个骨骼，之后便是一个个的骨骼，骨骼的大小不是固定的。主要包括了骨骼名字，父骨骼名字，初始旋转与初始平移、以及之后的各个旋转与平移关键帧。

在分析了解了MS3D的文件格式后，就可以通过编写程序读取MS3D文件并根据该文件建立模型了，对应于MS3D的不同分段，可以依次建立6种结构体分别对应每段内容：

MS3DHeader     /\*包含ms3d文件的版本信息\*
MS3DVertex     /\*顶点信息\*/
MS3DMaterial   /\*材质(纹理贴图等)信息\*/
MS3DTriangle   /\*绘制三角形信息\*/
MS3DJoint      /\*节点(骨骼)信息\*/
MS3DKeyframe   /\*关键窗口\*/
//an example for vertex
struct MS3DVertex
{
  unsigned char m_ucFlags;   //编辑器用标志
  CVector3 m_vVert;        //x,y,z的坐标
  char m_cBone;        //Bone ID （-1 ,没有骨头）
  unsigned char m_mcUnused;      //保留，未使用
};

(1)第一个成员表示了该顶点在编辑器中的状态（引擎中不是必须）其各个值的含义如下：

0：顶点可见，未选中状态

1：顶点可见，选中状态

2：顶点不可见，未选中状态

3：顶点不可见，选中状态

(2)第二个成员为顶点的坐标，CVector3为三个float型组成，总共12字节

(3)第三个成员为该顶点所绑定的骨骼的ID号，如果该值为-1 则代表没有绑定任何骨骼（静态）

(4)第四个成员不包含任何信息，直接略过。

将MS3D各段内容分别导入对应的结构体，将其读入内存。

多边形（三角形）结构读取示范：

//内存空间分配
// pPtr为文件读取偏移指针
int nTriangles = *( word* )pPtr;
m_numTriangles = nTriangles;
m_pTriangles = new Triangle[nTriangles];
pPtr += sizeof( word );
//读取每个三角型
for ( i = 0; i < nTriangles; i++ )
{
  MS3DTriangle *pTriangle = ( MS3DTriangle* )pPtr;
  int vertexIndices[3] = {
    pTriangle->m_vertexIndices[0], 
    pTriangle->m_vertexIndices[1], 
    pTriangle->m_vertexIndices[2] 
  };
  float t[3] = { 1.0f-pTriangle->m_t[0], 1.0f-pTriangle->m_t[1], 1.0f-pTriangle->m_t[2] };
  //数据读取
  memcpy( m_pTriangles[i].m_vertexNormals, pTriangle->m_vertexNormals, sizeof( float )*3*3 );
  memcpy( m_pTriangles[i].m_s, pTriangle->m_s, sizeof( float )*3 );
  memcpy( m_pTriangles[i].m_t, t, sizeof( float )*3 );
  memcpy( m_pTriangles[i].m_vertexIndices, vertexIndices, sizeof( int )*3 );
  //文件读取指针前进
  pPtr += sizeof( MS3DTriangle );
}

要注意得是，因为MS3D使用窗口坐标系而OpenGL使用笛卡儿坐标系，所以需要反转每个顶点Y方向的纹理坐标。

不同于之前的分类和聚类算法，优化的目的是尝试找到一个使成本函数输出最小化的值。这里主要包括两个算法：模拟退火算法和遗传算法。

成本函数:
接受一个经推测的题解，并返回一个数值结果，该值越大代表成本越高（题解表现越差），该值越小就表示题解越好。

模拟退火算法：

优化算法的目标可以看为寻找x使函数f(x)最小。

但是严格的最小值往往是很难达到的，我们不得不把眼光投入到寻找一个尽可能好的次优解去。

最简单的方法被称为随机法，即成千上万次的对x进行猜测，然后把这些x中使f(x)最小的一个作为答案。虽然这样很简单，但是效果很差。于是出现了爬山法。

爬山法从一个随机解出发，然后不断向该解附近的使f(x)的值更小的x移动，直到当前x附近的解都比x差为止。为了使效果更好，我们可以从多个随机解出发重复着一个过程，将最好的一个作为答案。很容易就能认识到，这样找到的解是一个极值点，是一个局部最小值。

爬山法虽然好，但是在其寻找最优解的过程中，前进的方向是固定的（使f(x)更小的方向），但是有时向其他方法前进也是必要的，因为f(x)可能先增大在变小成为最优的。

于是就有了模拟退火法。

该算法这源于固体的退火过程，即先将温度加到很高(大量原子被激发)，再缓慢降温(即退火)，则能使达到能量最低点。如果急速降温(即为淬火)则不能达到最低点。

模拟退火法同样是从一个随机解出发。但是它在寻找最优解时并不一定是向更好的x移动，也有一定的概率向更差的x移动，这个概率开始较大，但是会随时间而渐渐变小，直到稳定。一般该概率可以定义为：p=e ^ (-  (highcost – lowcost ) / temperature )，其中temperature是随时间增大而变小的温度，开始温度很高时p -> 1，后来会渐渐变小使p->0。

遗传算法：

遗传算法的思想来自生物的遗传和变异，算法以种群为单位（一个种群为一组既多个解），其算法的运行过程如下：

1. 随机生成一组初始解（初始种群）。
2. 计算种群中各个解的成本，然后进行排序。
3. 我们将种群中靠前（成本低）的解保留下来，删除其他解，这一过程称为精英选拔。
4. 对已有解进行微小的改变，将改变后的结果作为新的元素加入种群，这一过程称为变异。
5. 选择一些优秀的解两两组合，然后将他们按某种方式进行结合（如求平均），将得到的结果作为新的元素加入种群，这一过程称为交叉（配对）。
6. 不断重复2—5步，直到达到指定迭代次数或成本函数连续数代都没有更好的改善。
7. 得到一组解，该组解为算法输出。

该系列结束，恩，也许以后学了更多，有了更好的了解后会回来改一改，谁知道呢？

一直没有时间写…..唉

这个东西好像是属于数据可视化？反正就是把多维的数据降到低维空间但是仍然尽可能的保持原来数据之间的距离关系(就是在原来维度下离的远的点仍然离得远，接近的点仍然接近) 。最常见的应该就是降到2维以方便打印和屏幕输出。

算法的输入是所有数据在高维情况下两两之间的距离（记i与j的距离为Dij）。现在以降到2维为例说明这个算法。

首先我们把所有数据点随机绘制在一张二维图像上，然后计算它们两两之间的距离dij，然后我们计算出它与高维距离Dij的误差，根据这些误差，我们将每对数据点按比例移近或移远，然后重新计算所有dij，不断重复到我们没法减少误差为止。

还是来具体说明一下吧，假设有n个点

1. 输入每一对点之间的距离Dij。
2. 随机在2维平面生成n个点，点i坐标记为x[i]、y[i]，计算它们两之间的距离，记为dij.
3. 对所有i 和j计算：eij=(dij-Dij) / Dij，每个点用一个二维的值grad[k]来表示它要移动的距离的比例因子(初始为0,0)。在计算出每个eij后，计算 ((x[i]-x[j]) / dij)* eij，然后把它加到grad[i][x]上，同样把((y[i]-y[j]) / dij)* eij加到grad[i][y]上。
4. 把所有eij的绝对值相加，为总误差，与前一次的总误差比较(初始化为无穷大)，大于前一次的话就停止。否则把它作为上一次总误差，继续。
5. 对每个点，新的坐标为x[i] -= rate * grad[i][x]  y[i] -= rate*grad[i][y]，其中rate是开始时自己定义的一个常数参数，该参数影响了点的移动速度。重新计算各个dij，回到3。

伪码：

    for m = 1 to 1000{
      for i=1 to n
        for  j = 1 to n
          dij=sqrt((x[i] – x[j])^2+(y[i]-y[j])^2)
      for i=1 to n
        gradi=0
      totale=0
      for i= 1 to n
        for j= 1 to n{
           if(j==i) continue
             eij=(dij-Dij) / Dij
             grad[i][0]+= ((x[i] - x[j]) / dij)* eij
             grad[i][1]+=((y[i] - y[j]) / dij)* eij
             totale+=abs(eij)
           }
      if (laste < totale) break;
      laste=totale
      for i=1 to n{
        x[i] -= rate * grad[i][x]
        y[i] - = rate* grad[i][y]
      }
    }

因为这两个算法比较简单，又有些相似，所以这里放在一起。

K-最近邻：

k-最近邻也是一种用来进行预测的算法。

工作原理：

接受一个用以进行数值预测的新数据项，然后将它与一组已经赋过值的数据项进行比较。算法会从中找出与待预测数据最为接近的k项，并这k项其求均值以得到最终的结果。

总计来说这是一个很简单的算法，只要我们做好距离的定义并选择一个适合的k值，我们就可以很容易的实现它。

由于我们计算2组数据的距离的通常方法是将他们中对应的每一项目的差值的绝对值(或平方)相加，所以就会出现不同数据范围不同导致的误差。比如每组数据有2个分量，一个取值为0—10,另一个是0—-999999，那么第二的值就会几乎完全决定我们最后的结果。所以我们要对每一组数据进行缩放。

对数据的缩放取决于具体的应用，我们可以通过交叉验证尝试多组缩放因子然后比较它们的优劣。交叉验证的做法是先数据的一部分去除，然后用剩余数据去推测这组数据，我们就可以根据预测的结果对缩放因子进行评估。

优点：

能利用复杂函数进行数值预测，又简单易懂，并且我们可以很容易的在算法中实现查看用哪些近邻进行预测。

缺点：

每次进行预测，它都会使用所有样本，这会导致效率的低下。

寻找缩放因子是一项很乏味的工作.

聚类：

聚类算法可以用于任何具有一个或多个数值属性的数据集合，通过这些数值属性，我们将其所有数据映射到一个n维空间中，并定义该空间中的距离，然后我们可以通过各个数据间的距离对其实现聚类。

分级聚类:

分级聚类的算法是不断找出所有数据中距离最小的两个数据A、B，然后将它们合并成一个新的节点，该节点在n维空间中的坐标是原来两数据点的均值，通过不断进行这一操作，我们最终可以得到一个树形的层级结构。

K-均值聚类:

不同于分级聚类，K-均值聚类的目的是将数据拆成K个不同的群组，其具体算法如下：

1. 在n维空间中随机生成K个中心点
2. 将每个数据项分配给与其距离最近的中心点。
3. 将中心点位置移动到所有分配给它的数据项的中心。如果中心点位置没有改变，则结束算法，否则回到第二步。

具体选择哪种聚类算法取决于要处理的问题，当要将数据拆分到不同的群组时，k均值聚类往往是很有价值的，而如果我们更想了解哪些群组间更为接近，分级聚类更好。当然，我们也可以同时使用２种算法得到更加详细的信息。

      今天上了开学的第一节统计学，开了很久的小差，想了不少东西。

      以前虽然自学过概率论与数理统计，但是也只是了解了一些公式与原理，一直对于统计学的一些应用不甚理解(或者说不能接受)，尤其是基于统计的机器学习，一直不能接受它作为一种实现的人工智能的手段。因为我心中的人工智能是绝对理性，严谨，逻辑的。虽然我可以接受统计学的理论，却不能把它作为一种严谨的逻辑。

　 但是，今天突然想到了感性，是的，人是理性的，但是人的思维中也充满了感性的，当然，这是早已熟知的事实。

　 先给感性下一个定义吧。

　 感性：作用于人的感觉器官而产生的感觉，知觉和表象等直观认识，相对与‘理性’”

　 是的，感性一种直观的认识，那么这种认识从哪里来呢？过去的经验。人们的感性是在经验的基础上建立的，是一种仅仅由经验得出而没有任何逻辑背景的判断。

　 统计学不也是这样么？将大量的样本作为过去的经验，仅仅由这些经验而不带任何逻辑推断的去快速做出一种“感性”的判断。只是这种感性比人的感性更加严谨，不会受到类似“小概率事件经常发生”这种错觉的影响，但也可以算是一种理性的感性了。

      对应的，我又想起了逻辑学，如果统计是根据经验快速简单的做出判断的话，那么逻辑学就是通过严谨的逻辑推理去寻找正确的答案，这个过程会很繁琐，但是它使绝对严谨理性的，比我们的大脑更加严谨，理性——那何不把它看成一种是理性的理性呢？

     但是仅仅有统计与逻辑，我们无法建立一个系统，因此也许还需要一个驱动吧？在完成一个任务、解决一个问题时，这个驱动不断的让感性提供可能解，然后让理性验证它——突然我发现，这不就是“启发式搜索”所作的事情么？

     以前翻过一些人工智能的书，总是觉的虽然那些方法可以达到目的，但是却没有触及到智能的本质，因此总是有些失望的，可是现在，我释然了。什么是智能的本质？好像是在《与众不同的心理学》这本书上，我看到过类似问题(也许问得是别的什么，不过差不多)。书里说，这是不可验证的，如果我们甚至不能解释，验证它，我们为什么可以凭借自己的主观推断去确定一个机器是否拥有智能？我们凭什么可以认为，这些机器，当他们把现在这些技术发挥到一定程度后就不可以拥有智能？也许我们自己的自我认知也只是一种数学的算法对自身产生的作用呢？（是不是有谁说过，这个宇宙，连同我们的存在，都只是一种错觉？记不清了…..不过看来这句话还是很有意思的。）

　 想到了这些之后，我对“人工智能最难的是处理常识”第一次有了很深的认同，以前总是不能充分认识常识的作用，但是如果直觉，经验在智能中占了如此重要的一部分，那么我们就必须去处理常识――其中的困难自然不用多说了。

     最后，把我上课时写在书上的话记录下来吧：

     统计学—以理性研究感性，我们的直觉从过去的经验去推导未来，这种推断不能解释结果的原因。（因为它在历史上倾向于如此，所以它很可能如此。）统计学将这种感性理性化，并出除了一些直觉上的错误（如：小概率事件经常发生），但其根本上还是一种感性的判断，因此解释这种感性推断背后的原因，事物呈现这种状态的原因，就是人的工作了。所以统计学也可以用来在没有线索时，作为一种“事后诸葛亮”式的推断的第一步（即先找出最可能答案，在设法解释它，不过这种方法具有不可证伪性，所以不是科学严谨的――毕竟是直觉么）。同时，统计的机器学习可以就可用来模拟人的直觉学习了（而且是一种没有错误的直觉）。